Agujero de gusano

Esquema de un agujero de gusano que técnicamente permite el viaje a través del tiempo. Si uno de los dos extremos del puente atravesado por la línea verde está en movimiento, seguir la ruta roja y volver al punto inicial según en sentido opuesto a la ruta verde podría permitir volver atrás en el tiempo, ya que el espacio-tiempo representado contendría curvas temporales cerradas.

En física, un agujero de gusano, también conocido como puente de Einstein-Rosen, es una estructura hipotética asociada a un espacio-tiempo cuya topología es múltiplemente conexa. Dicha estructura es una solución posible de las ecuaciones de campo de Einstein de la relatividad general, que esencialmente consiste en un puente a través del espacio y el tiempo. Un agujero de gusano tiene por lo menos dos extremos conectados a una única garganta, a través de la cual podría desplazarse la materia. Hasta la fecha no se ha hallado ninguna evidencia de que el espacio-tiempo conocido contenga estructuras de este tipo, por lo que en la actualidad es solo una posibilidad teórica en la física.

Cuando una estrella supergigante roja explota, arroja materia al exterior, de modo que acaba siendo de un tamaño inferior y se convierte en una estrella de neutrones. Pero también puede suceder que se comprima tanto que absorba su propia energía en su interior y desaparezca dejando un agujero negro en el lugar que ocupaba. Este agujero tendría una gravedad tan grande que ni siquiera la radiación electromagnética podría escapar de su interior. Estaría rodeado por una frontera esférica, llamada horizonte de sucesos. La luz traspasaría esta frontera para entrar, pero no podría salir, por lo que el agujero visto desde grandes distancias debería ser completamente negro (aunque Stephen Hawking postuló que ciertos efectos cuánticos generarían la llamada radiación de Hawking). Dentro del agujero los astrofísicos conjeturan que se forma una especie de cono sin fondo. En 1994, el telescopio espacial Hubble detectó la presencia de uno muy denso en el centro de la galaxia elíptica M87, pues la alta aceleración de gases en esa región indica que debe haber un objeto 3500 millones de veces más masivo que el Sol. Finalmente, este agujero podría terminar por absorber a la galaxia entera.​

La hipótesis sugiere que, de un lado, hay un agujero negro que absorbe la materia, pero, por el otro lado, habría un agujero blanco que expulsaría todo lo que traga el negro.

El primer científico en advertir de la existencia de agujeros de gusano fue el austríaco Ludwig Flamm, en 1916. En este sentido, la hipótesis del agujero de gusano es una actualización de la decimonónica teoría de una cuarta dimensión espacial que suponía —por ejemplo—, dado un cuerpo toroidal en el que se podían encontrar las tres dimensiones espaciales comúnmente perceptibles, una cuarta dimensión espacial que abreviara las distancias y, de esa manera, los tiempos de viaje. Esta noción inicial fue planteada de manera más científica en 1921 por el matemático alemán Hermann Weyl, sin embargo, no usó el término "agujero de gusano" (habló de "tubos unidimensionales"), cuando este relacionó sus análisis de la masa en términos de la energía de un campo electromagnético​ con la teoría de la relatividad de Albert Einstein publicada en 1916.

En la actualidad, la teoría de cuerdas admite la existencia de más de tres dimensiones espaciales (ver hiperespacio), pero esas dimensiones extra estarían compactadas a escalas subatómicas (según la teoría de Kaluza-Klein), por lo que parece muy difícil (si no imposible) aprovecharlas para emprender viajes en el espacio y el tiempo.

Origen del nombre

El término «agujero de gusano» fue introducido por el físico teórico estadounidense John Wheeler en 1957 (inspirado en la obra de Hermann Weyl) y mediante un artículo coescrito con Charles Misner:​

Este análisis obliga a considerar situaciones ... donde hay un flujo neto de líneas de fuerza, a través de lo que los topólogos llamarían "descomposición toroidal" del espacio con múltiples conexiones, y qué los físicos tal vez podrían excusarse para denominar más vívidamente un "agujero de gusano".

Charles Misner y John Wheeler en Annals of Physics

Proviene de la siguiente analogía usada para explicar el fenómeno: si el universo es la piel de una manzana, y un gusano viaja sobre su superficie, la distancia de un punto de la manzana a su antípoda es igual a la mitad de la circunferencia de la manzana, siempre que el gusano permanezca sobre la superficie de ésta. Pero si en vez de esto, el gusano cavara un agujero directamente a través de la manzana, la distancia que tendría que recorrer sería considerablemente menor, ya que la distancia más cercana entre dos puntos es una línea recta que une a ambos.

Tipos de agujero de gusano

• Los agujeros de gusano del intrauniverso conectan una posición de un universo con otra posición del mismo universo en un tiempo diferente. Un agujero de gusano debería poder conectar posiciones distantes en el universo por plegamientos espaciotemporales, de manera que permitiría viajar entre ellas en un tiempo menor que el que tomaría hacer el viaje a través del espacio normal.
• Los agujeros de gusano del interuniverso asocian un universo con otro diferente y se denominan «agujeros de gusano de Schwarzschild». Esto permite especular sobre si tales agujeros de gusano podrían usarse para viajar de un universo a otro paralelo. Otra aplicación de un agujero de gusano podría ser el viaje en el tiempo. En ese caso, sería un atajo para desplazarse de un punto espaciotemporal a otro. En la teoría de cuerdas, un agujero de gusano es visto como la conexión entre dos D-branas, donde las bocas están asociadas a las branas y conectadas por un tubo de flujo. Se cree que los agujeros de gusano son una parte de la espuma cuántica o espaciotemporal.

Otra clasificación:

• Los agujeros de gusano euclídeos, estudiados en física de partículas.
• Los agujeros de gusano de Lorentz, principalmente estudiados en relatividad general y en gravedad semiclásica. Dentro de estos destacan los agujeros de gusano atravesables, un tipo especial de agujero de gusano de Lorentz que permitiría a un ser humano viajar de un lado al otro del agujero.

Hasta el momento se ha teorizado sobre diferentes tipos de agujeros de gusano, principalmente como soluciones matemáticas a la cuestión. Esencialmente, estos tipos de agujero de gusano son:

• El agujero de gusano de Schwarzschild supuestamente formado por un agujero negro de Schwarzschild, que se considera infranqueable.
• El agujero de gusano supuestamente formado por un agujero negro de Reissner-Nordstrøm o Kerr-Newman, que resultaría franqueable, pero en una sola dirección, y que podría contener un agujero de gusano de Schwarzschild.
• El agujero de gusano de Lorentz, que posee masa negativa y se estima franqueable en ambas direcciones (pasado y futuro).

Agujeros de gusano de Schwarzschild

Diagrama de un agujero de gusano de Schwarzschild.

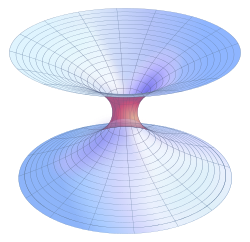
Los agujeros de gusano de Lorentz, conocidos como agujeros de gusano de Schwarzschild o puentes de Einstein-Rosen, son nexos que unen áreas de espacio que puede ser modeladas como soluciones de vacío en las ecuaciones de campo de Einstein por unión de un modelo de agujero negro y uno de agujero blanco. Esta solución fue hallada por Albert Einstein y su compañero Nathan Rosen, que publicó primero el resultado en 1935. Sin embargo, en 1962, John A. Wheeler y Robert W. Fuller publicaron un artículo en el que divulgaban la demostración de que este tipo de agujero de gusano es inestable y se desintegraría instantáneamente tan pronto como se formase.

Antes de que los problemas de estabilidad de los agujeros de gusano de Schwarzschild se hiciesen evidentes, se propuso que los cuásares podían ser agujeros blancos, de modo que formaban las zonas terminales de los agujeros de gusano de este tipo. Sin embargo, investigaciones recientes descartan que los cuásares sean equiparables a los agujeros blancos.

Los agujeros de gusano de Schwarzschild inspiraron a Kip Thorne a imaginar el tránsito por ellos mediante la sujeción de su garganta y su apertura por medio de materia exótica (de masa y energía negativas).

Agujeros de gusano practicables

Imagen de un agujero de gusano practicable (que se puede atravesar) que conectaría el área frente al instituto de física de la Universidad de Tubinga con las dunas próximas a Boulogne-sur-Mer, en el norte de Francia. La imagen ha sido recreada mediante un software de trazado de rayos en 4D, en una métrica de Morris-Thorne, aunque los efectos gravitatorios sobre la longitud de onda no se han simulado.​

Los agujeros de gusano practicables de Lorentz, también llamados atravesables, permitirían viajar no solo de una parte del universo a otra, sino incluso de un universo a otro. Los agujeros de gusano conectan dos puntos del espacio-tiempo, por lo que permitirían el viaje tanto en el espacio como en el tiempo. En la teoría de la relatividad general, la posibilidad de atravesar agujeros de gusano fue demostrada por primera vez por Kip S. Thorne y su graduado Mike Morris en un artículo publicado en 1988. El tipo de agujero de gusano atravesable que ellos descubrieron se mantendría abierto por una especie de concha esférica de materia exótica denominada agujero de gusano de Morris-Thorne. Posteriormente se han descubierto otros tipos de agujeros de gusano atravesables, como uno que se mantiene abierto por cuerdas cósmicas, ya hipotetizado antes por Matt Visser en un artículo publicado en 1989.

Base teórica

Definición

La definición topológica de agujero de gusano no es nada intuitiva. Se dice que en una región compacta del espacio-tiempo existe un agujero de gusano cuando su conjunto frontera es trivial desde el punto de vista topológico, pero su interior no es simplemente conexo. Formalizar esta idea conduce a definiciones como la siguiente, tomada del Lorentzian Wormholes, de Matt Visser:

Si un espacio-tiempo de Lorentz contiene una región compacta Ω y si la topología de Ω es de la forma Ω ~ R x Σ, donde Σ es una 3-variedad de topología no trivial, cuya frontera tiene topología de la forma dΣ ~ S², y si además las hipersuperficies Σ son de tipo espacial, entonces la región Ω contiene un agujero de gusano intrauniversal cuasipermanente.

Caracterizar agujeros de gusano del interuniverso es más difícil. Por ejemplo, podemos imaginar un universo recién nacido conectado a su progenitor por un ombligo estrecho. Cabría considerar el ombligo como la garganta de un agujero de gusano, por la cual el espacio-tiempo está conectado.

Plausibilidad

Se sabe que los agujeros de gusano de Lorentz son posibles dentro de la relatividad general, pero la posibilidad física de estas soluciones es incierta. Incluso, se desconoce si la teoría de la gravedad cuántica, que se obtiene al condensar la relatividad general con la mecánica cuántica, permitiría la existencia de estos fenómenos. La mayoría de las soluciones conocidas de la relatividad general que permiten la existencia de agujeros de gusano atravesados requieren la existencia de materia extraña, una sustancia teórica que contiene energía de densidad negativa. Sin embargo, no ha sido matemáticamente probado que este sea un requisito absoluto para este tipo agujeros de gusano atravesados ni se ha establecido que la materia exótica no puede existir.

Aún no se sabe empíricamente si existen agujeros de gusano. Una solución a las ecuaciones de la relatividad general (tal como la que encontrara L. Flamm) que hiciera posible la existencia de un agujero de gusano sin el requisito de una materia exótica —sustancia teórica que poseería una densidad de energía negativa— no ha sido todavía verificada. Muchos físicos, incluido Stephen Hawking (con su conjetura de protección cronológica), consideran que a causa de las paradojas (¿o acaso aporías?) un viaje en el tiempo a través de un agujero de gusano implicaría que existiera algo fundamental en las leyes de la física que impida tales fenómenos (ver censura cósmica).

En marzo de 2005, Amos Ori visualizó un agujero de gusano que permitía viajar en el tiempo sin requerir materia exótica y satisfaciendo todas las condiciones energéticas. La estabilidad de esta solución es incierta, por lo que sigue sin quedar claro si se requeriría una precisión infinita para que se formase y permitiese el viaje en el tiempo y si los efectos cuánticos protegerían la secuencia cronológica del tiempo en este caso.

Métrica de los agujeros de gusano

Las teorías sobre la métrica de los agujeros de gusano describen la geometría del espacio-tiempo de un agujero de gusano y sirven de modelos teóricos para el viaje en el tiempo. Un ejemplo simple de la métrica de un agujero de gusano atravesado podría ser el siguiente:​

$ds^{2}=-c^{2}{\text{d}}t^{2}+{\text{d}}l^{2}+(k^{2}+l^{2})({\text{d}}\theta ^{2}+\sin ^{2}\theta \,{\text{d}}\phi ^{2})$

Un tipo de métrica de agujero de gusano no atravesado es la solución de Schwarzschild:

$ds^{2}=-\left(1-{\frac {2GM}{c^{2}r}}\right){\text{d}}t^{2}+{\frac {{\text{d}}r^{2}}{1-{\cfrac {2GM}{c^{2}r}}}}+r^{2}({\text{d}}\theta ^{2}+\sin ^{2}\theta \,{\text{d}}\phi ^{2})$

representado por primera vez por Ellis como un caso especial de drenaje de Ellis.

El puente de Einstein-Rosen se describió en un artículo publicado en julio de 1935.​​

Para la solución estática simétricamente esférica de Schwarzschild.

$ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+(1-{\frac {2m}{r}})dt^{2}$

($ds$ = momento apropiado, $c$ = 1)

Si uno reemplaza $r$ por $u$ según $u^{2}=r-2m$

El espacio de cuatro dimensiones se describe matemáticamente mediante dos partes congruentes u "hojas", que corresponden a $u$ > 0 y $u$ < 0, que están unidas por un hiperplano $r=2m$ o $u$ = 0 en el que $g$ desaparece. Llamamos a tal conexión entre las dos hojas un "puente" (autores=A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity")

Para la combinación gravedad y electricidad, Einstein y Rosen derivaron la solución esférica simétrica de Schwarzschild

$\phi _{1}=\phi _{2}=\phi _{3}=0,\phi _{4}={\frac {\epsilon }{4}},$

$ds^{2}=-{\frac {1}{(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}})}}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}})dt^{2}$

($\epsilon$ = carga eléctrica)

Las ecuaciones de campo sin denominadores en el caso en que $m$ = 0 se pueden escribir

$\phi _{\mu \nu }=\phi _{\mu ,\nu }-\phi _{\nu ,\mu }$

$g^{2}\phi _{\mu \nu ;\sigma }g^{\nu \sigma }=0$

$g^{2}(R_{ik}+\phi _{i\alpha }\phi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\phi _{\alpha \beta }\phi ^{ab})=0$

Para eliminar las singularidades, si se reemplaza $r$ por $u$ según la ecuación:

$u^{2}=r^{2}-{\frac {\epsilon ^{2}}{2}}$

y con $m$ = 0 se obtiene​​

$\phi _{1}=\phi _{2}=\phi _{3}=0,\phi _{4}=\epsilon /(u^{2}+{\frac {\epsilon ^{2}}{2}})^{\frac {1}{2}}$

$ds^{2}=-du^{2}-(u^{2}+{\frac {\epsilon ^{2}}{2}})(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+({\frac {2u^{2}}{2u^{2}+\epsilon ^{2}}})dt^{2}$

La solución está libre de singularidades para todos los puntos finitos en el espacio de las dos hojas (autores=A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity")

Agujeros de gusano y viajes en el tiempo

Interpretación artística de un agujero de gusano como debiera ser visto por un observador que estuviera atravesando el horizonte de sucesos de un agujero de gusano de Schwarzschild, que es similar a un agujero negro de Schwarzschild, pero con la peculiaridad de poseer, en vez de la región en que se debiera encontrar la singularidad gravitacional (en el caso del agujero negro), un camino inestable hacia un agujero blanco que existiría en otro universo (véase multiverso). Esta región es inaccesible en el caso de un agujero de gusano de Schwarzschild en cuanto que el puente entre el agujero negro y el blanco colapsaría siempre antes de que el observador tenga tiempo de atravesarlo. Véase White Holes and Wormholes para una discusión más técnica y una animación que representa lo que un observador vería atravesando un agujero de gusano de Schwarzschild.

En teoría, un agujero de gusano podría permitir viajar en el tiempo a través del espacio-tiempo. Esto podría llevarse a cabo acelerando el extremo final de un agujero de gusano a una velocidad relativamente alta respecto de su otro extremo. La dilatación de tiempo relativista resultaría en una boca del agujero de gusano acelerada envejeciendo más lentamente que la boca estacionaria, visto por un observador externo, de forma parecida a lo que se observa en la paradoja de los gemelos. Sin embargo, el tiempo pasa diferente a través del agujero de gusano respecto del exterior, por lo que los relojes sincronizados en cada boca permanecerán sincronizados para alguien viajando a través del agujero de gusano, sin importar cuanto se muevan las bocas. Esto quiere decir que cualquier cosa que entre por la boca acelerada del agujero de gusano podría salir por la boca estacionaria en un punto temporal anterior al de su entrada si la dilatación de tiempo ha sido suficiente.

Por ejemplo, supongamos que dos relojes en ambas bocas muestran el año 2000 antes de acelerar una de las bocas y, tras acelerar una de las bocas hasta velocidades cercanas a la de la luz, juntamos ambas bocas cuando en la boca acelerada el reloj marca el año 2017 y en la boca estacionaria marca el año 2013. De esta forma, un viajero que entrara por la boca acelerada en este momento saldría por la boca estacionaria cuando su reloj también marcara el año 2013, en la misma región del espacio pero cuatro años en el pasado. Tal configuración de agujeros de gusano permitiría a una partícula de la Línea de universo del espacio-tiempo formar un circuito espacio-temporal cerrado, conocido como curva cerrada de tipo tiempo. El curso a través de un agujero de gusano a través de una curva cerrada de tipo tiempo hace que un agujero de gusano tenga características de hueco temporal.

Se considera que es prácticamente imposible convertir a un agujero de gusano en una «máquina del tiempo» de este modo. Algunos análisis usando aproximaciones semiclásicas que incorporan efectos cuánticos en la relatividad general señalan que una retroalimentación de partículas virtuales circularían a través del agujero de gusano con una intensidad en continuo aumento, destruyéndolo antes de que cualquier información pudiera atravesarlo, de acuerdo con lo que postula la conjetura de protección cronológica. Esto ha sido puesto en duda, sugiriendo que la radiación se dispersaría después de viajar a través del agujero de gusano, impidiendo así su acumulación infinita. Kip S. Thorne mantiene un debate al respecto en su libro Agujeros negros y tiempo curvo (Black Holes and Time Warps).​ También se ha descrito el denominado Anillo Romano, una configuración formada por más de un agujero de gusano. Este anillo parece permitir una línea de tiempo cerrado con agujeros de gusano estables cuando es analizado bajo el prisma de la gravedad semiclásica, pero sin una teoría completa de la gravedad cuántica aún no se puede saber si dicha aproximación semiclásica es aplicable en este caso.

Viajes a velocidades superiores a la de la luz

La relatividad especial solo tiene aplicación localmente. Los agujeros de gusano — si en efecto existiesen— permitirían teóricamente el viaje superluminal (más rápido que la luz) asegurando que la velocidad de la luz no es excedida localmente en ningún momento. Al viajar a través de un agujero de gusano, las velocidades son subluminales (por debajo de la velocidad de la luz). Si dos puntos están conectados por un agujero de gusano, el tiempo que se tarda en atravesarlo sería menor que el tiempo que tarda un rayo de luz en hacer el viaje por el exterior del agujero de gusano. Sin embargo, un rayo de luz viajando a través del agujero de gusano siempre alcanzaría al viajero. A modo de analogía, rodear una montaña por el costado hasta el lado opuesto a la máxima velocidad puede tomar más tiempo que cruzar por debajo de la montaña a través de un túnel a menor velocidad, ya que el recorrido es más corto.

Subatómicamente se hipotetiza la existencia de una espuma cuántica o de una espuma de espacio-tiempo, avanzando con la conjetura, se hipotetiza la posibilidad de existencia de agujeros de gusano en la misma, aunque si estos existieran serían altamente inestables y solo se podrían estabilizar invirtiendo enormes cantidades de energía (por ejemplo con aceleradores de partículas gigantescos que puedan crear un plasma de quarks-gluones).

Viaje interuniversal

Una posible resolución de las paradojas resultantes de los viajes en el tiempo a través de los agujeros de gusano se basa en la interpretación de los muchos mundos.

En 1991, David Deutsch demostró que la teoría cuántica es totalmente coherente (en el sentido de que la llamada matriz de densidad puede estar libre de discontinuidades) en períodos de tiempo con curvas cerradas de tiempo.​ Sin embargo, más tarde se demostró que dicho modelo de curva de tiempo cerrado puede tener inconsistencias internas, ya que conducirá a fenómenos extraños como la distinción de estados cuánticos no ortogonales y la distinción de la mezcla adecuada e inadecuada.​​ Por consiguiente, se evita el bucle de retroalimentación positiva destructiva de partículas virtuales que circulan a través de una máquina de tiempo de agujero de gusano, un resultado indicado por cálculos semi-clásicos. Una partícula que regresa del futuro no regresa a su universo de origen sino a un universo paralelo. Esto sugiere que una máquina de tiempo de agujero de gusano con un salto de tiempo extremadamente corto es un puente teórico entre universos paralelos contemporáneos.​

Debido a que una máquina del tiempo de agujero de gusano introduce un tipo de no linealidad en la teoría cuántica, este tipo de comunicación entre universos paralelos es consistente con la propuesta de Joseph Polchinski de un teléfono Everett​ (llamado así por Hugh Everett) en la formulación de Steven Weinberg de la mecánica cuántica no lineal.​

La posibilidad de comunicación entre universos paralelos se ha denominado viajes interuniversales.​

Véase también

• Agujero negro
  • Agujero negro supermasivo
  • Microagujero negro
• Agujero negro de Schwarzschild
• Agujero negro en rotación
• Agujero blanco
• Espuma cuántica
• John Wheeler
• Kip S. Thorne
• Kepler 452b
• Gravastar
• Conjetura de protección cronológica
• Multiverso
• Espacio-Tiempo

Referencias

Bibliografía

• DeBenedictis, Andrew and Das, A. «On a General Class of Wormhole Geometries». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Dzhunushaliev, Vladimir. «Strings in the Einstein's paradigm of matter». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Einstein, Albert and Rosen, Nathan. The Particle Problem in the General Theory of Relativity. Physical Review 48, 73 (1935).
• Fuller, Robert W. and Wheeler, John A.. Causality and Multiply-Connected Space-Time. Physical Review 128, 919 (1962).
• Garattini, Remo. «How Spacetime Foam modifies the brick wall». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• González-Díaz, Pedro F. «Quantum time machine». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• González-Díaz, Pedro F. «Ringholes and closed timelike curves». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Khatsymosky, Vladimir M. «Towards possibility of self-maintained vacuum traversable wormhole». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Krasnikov, Serguei. «Counter example to a quantum inequality». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Krasnikov, Serguei. «The quantum inequalities do not forbid spacetime shortcuts». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Li, Li-Xin. «Two Open Universes Connected by a Wormhole: Exact Solutions». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Morris, Michael S., Thorne, Kip S., and Yurtsever, Ulvi. Wormholes, Time Machines, and the Weak Energy Condition. Physical Review Letters 61, 1446–1449 (1988).
• Morris, Michael S. and Thorne, Kip S.. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).. American Journal of Physics 56, 395-412 (1988).
• Nandi, Kamal K. and Zhang, Yuan-Zhong. «A Quantum Constraint for the Physical Viability of Classical Traversable Lorentzian Wormholes». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Ori, Amos. «A new time-machine model with compact vacuum core». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Roman, Thomas, A. «Some Thoughts on Energy Conditions and Wormholes». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Teo, Edward. «Rotating traversable wormholes». arXiv eprint server. Consultado el 12 de agosto de 2005. 
• Visser, Matt. «The quantum physics of chronology protection by Matt Visser.». arXiv eprint server. Consultado el 12 de agosto de 2005.  A more concise review.
• Visser, Matt. Traversable wormholes: Some simple examples. Physical Review D 39, 3182–3184 (1989).

Enlaces externos

• La Física de los Viajes en el Tiempo a través de un Agujero de gusano Archivado el 21 de abril de 2018 en Wayback Machine. por Raúl Isea.
• Creating a Traversable Wormhole por Mohammad Mansouryar (en inglés).
• ¿Qué es exactamente un agujero de gusano? respuesta de Richard F. Holman, William A. Hiscock y Matt Visser (en inglés).
• ¿Por qué agujeros de gusano? por Matt Visser (en inglés).
• Agujeros de gusano en la relatividad general por Soshichi Uchii (en inglés).
• Nuevos agujeros de gusano mejorados por John G. Cramer (en inglés).
• Tiempo, viaje en el tiempo y agujeros de gusano atravesados incluye un foro de discusión (en inglés).
• Agujeros blancos y agujeros de gusano presenta una descripción de los agujeros de gusano de Schwarzschild con gráficos y animaciones, por Andrew J. S. Hamilton (en inglés).
• Wormhole on arxiv.org
• Scientific American Magazine (December 2005 Issue) Wormhole Un juego sobre agujeros de gusano (en inglés).
• Wormhole MUD - A Sci-Fi Multi-User Dungeon

• Datos: Q7544
• Multimedia: Wormholes / Q7544